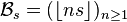从左到右DP, 存储哪里有奶牛以后排序, 同一个x坐标的上下奶牛合并.. 0没有 1上 2下 3都有
随着奶牛的位置x从左到右DP, 需要记录的状态是dp[i][p][k], p是在x处的奶牛圈起来的方式, 我记的是 0没圈(这就初始状态可能) 1圈上 2圈下 3两个一起圈 4两个分开圈, 记录每个可能的k和对应的面积最小值
状态转移比较麻烦.. 我是又分两个状态之间的圈圈怎样互相结合来枚举, 0不结合 1上边延伸出去 2下边 3两边一起延伸 4两边分开延伸. 应该还有更巧妙的方法.. 不想再碰这题了
172ms 直接大数组20M内存..代码点下面
Continue reading
挺简单的算法我没想出来..
考虑最左边的需要移除墙的列。这列是必定要移除一些墙的。
不妨移除右边界较大的那些墙。
实现的时候，可以用基数排序的方式来找到右边界较大的墙。
开两个数组如下：
map[i][j] = { 第i列中，从该列开始向右延伸，长度为j的墙的数目}
cnt[i] = {第i列中墙的数目}
这样代码比较方便，速度也快。 ——荣誉属于糯米
糯米的这个数据结构非常棒, 我做了一点改进: 糯米记录了右边还有多长的墙, 实际上只要记录右边墙的边界就可以了, 省掉一些计算和思维复杂度
所以我的代码精简一点, 看我的吧 🙂
这种题一眼看上去像DP, 我看了点东西说DP和贪心有很多相似之处, 比如都是找最优子结构. 区别在于贪心从最优子结构里选出一个或几个就行. 具体有什么区别也没太搞清楚, 感觉DP有一个图的延伸, 每个状态都可能被多次使用, 而贪心不会.
代码点下面:
Continue reading
这两道题用的理论都是一样的, 贪心算法很简单, 关键是怎么证明:
首先需要了解的是..
序理论(中文) http://zh.wikipedia.org/zh-sg/%E5%BA%8F%E7%90%86%E8%AE%BA
偏序集(中文) http://zh.wikipedia.org/zh-sg/%E5%81%8F%E5%BA%8F%E5%85%B3%E7%B3%BB
Dilworth’s Theorem(wiki没中文) http://en.wikipedia.org/wiki/Dilworth’s_theorem
Dilworth的对偶定理的证明我看的lambda2fei牛这里写的, 英文太长实在是没法看..
Dilworth本身的证明我还没有看.. TODO. 但是lamb牛写的chain(链)和antichain(反链)的转换我一看就明了, 通过这种转换可以很容易的使用Dilworth定理, 同样也可以证明Dilworth定理, 我还没看原本怎么证明的..(稍后update) 这种方法已经很牛逼了感觉
为了文章完整性引用一下他的证明
Dilworth定理说的是：对于一个偏序集，其最少链划分数等于其最长反链的长度。
Dilworth定理的对偶定理说的是：对于一个偏序集，其最少反链划分数等于其最长链的长度。
Dilworth定理先不证，有空再不上来，其对偶定理证明如下：设一个偏序集S的最少反链划分数是p，最长链长度是r。
1.先证p≥r。这是显然的，因为最长链长度是r，r个元素中的任意两个都可以比较，因此它们必定两两属于不同的反链，因此反链个数≥r，即p≥r。
2.再证r≥p。设X1=S。找出X1的所有极小元组成集合Z1，将其从X1删之，得到X2，再找出X2的所有极小元组成集合Z2（特别注意Z2中的任何元素a2，在X1中必然存在一个元素a1使得a1≤a2，否则a2可以放到X1中，这与X1的选取矛盾），再将Z2从X2中删除，得到X3，……这样一直下去，总存在一个k使得XK不空但X(K+1)为空。这样便得到一条链a1，a2，a3，……，ak，其中ai属于Xi。由于r是最长链长度，因此r≥k。另一方面，我们也得到了一个反链划分，即X1，X2，X3，……，XK。由于p是最少反链划分，因此k≥p。因此有r≥p。证毕。
要求的就是集合的chain的划分最小数目.
对于题目中给出的关系P={l <= l’ and w <= w’}, 我们定义关系P’={l < l’ and w > w’} (并不是l<=l’), 那么对于原来关于 P 可比较的两个元素, 关于 P’ 则不能比较, 原来不能比较关于 P’ 就可比较. 相应的 P 的 chain/antichain 就成为 P’ 的 antichain/chain .
这样定义后, 就可以放下原题, 题目变成找一堆元素中的最少antichain数目, 根据Dilworth定理对偶定理的证明过程(如上), 每次剥离出 Xi 中的所有极小元, 直到 Xi 为空, 剥离的次数就是答案 .
剥离的次数 == k== 关于 P’ 的最长chain的长度(对偶定理) == 关于P的最长antichain的长度(chain转换) == 关于P的chain的最少划分数(Dilworth)
有点绕.. 但比看上去简单
实例:
考虑元素集 (1,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,5) (4,1) (5,2) (6,1) (6,7) (7,1)
每次取出关于 P’ 的极小元, 过程如下
[cpp]
(1,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,5) (4,1) (5,2) (6,1) (6,7) (7,1)
(3,1) (3,2) (3,3) (4,1) (5,2) (6,1) (7,1)
(4,1) (5,2) (6,1) (7,1)
(6,1) (7,1)
[/cpp]
因为P’是严格的偏序关系, 每次取出的最小元 x 就要满足找不到 y 使 y P’ x (如果是不严格的偏序就要考虑自反的情况)
怎样取极小元呢, P’ 的极小元是 “在 l 比它小的元素中, 找不到 w 比它大的元素”, 按照代码中的 comp() 排序以后(先l后w), 以这个条件找极小元的集合, 等价于从第一个元素开始找, 后一个元素的w’>=前一个元素的w, 的元素集合. 比如(1,2) (2,3) (2,4) (3,5) (6,7), 满足2<=3<=4<=5<=7, 这样贪心就很简单了
和1065基本一样, 有了上面的理论就很好做了. 关键在于 P => P’ 的转换
P={w1<w2 && h1<h2} (大于小于无所谓)
所以 P的”可比较”关系 Pc = {w<w2 && h1<h2 || w1>w2 && h1>h2}
所以 P’c= {w1<w2 && w1>=h2 || w1>w2 && h1<=h2 || w1==w2}
所以 P’= {w1<=w2 && h1>=h2}
这里 P’ 是具有自反性和反对称性的非严格偏序关系.
这里就有一个问题: 集合内元素具有互异性, 但是题目中的元素有可能存在两两相同的, 怎么办?
我们可以想像我们上面讨论的集合是题目中的元素”只保留相同元素中的一个”后的集合, 这个集合中的元素a包含了n个题目中的相同元素, 就有两种处理的方法:
方法一: 把这n个元素看作一个a来”剥离”(取最小元), 1065就是这样, (1,2)(1,2)(1,2)在一起剥离是可以的, 因为1<=1,2<=2, 符合P的比较条件
方法二: 剥离a后a还存在于后来的Xi中, 并且n-=1, 直到n==0 a消失, 3636就要这么干, (1,2)(1,2)是不能放在一起的, 不符题意(P), 可以证明这样干是最优的(如果不取这个最小元, 这次执行后得到的Xi要比取的元素多一个, 不取白不取)
经过思考, 这道题最终要做的贪心是: 先按照w排序, w的互异值从小到大为w1,w2..wk, 然后在w==w1的元素里找到h最大的元素取出, 再在w2中找h最大的元素取出, 并且这些h需要满足条件:比前一个取出的元素的h大, 取完一次result++, 直到取空
代码点下面:
Continue reading
好繁的一道题.. 看走眼了 1061才是数论题..才发现 思路:
区域看作一个Vertex, 对每个区域BFS求出能到达所有club的和最小值. 复杂度N2
Edge的构造: 一个region周围的点集按顺时针是 {p1, p2, p3 .. pk} 那么 (p1, p2) (p2, p3) … (p(k-1), pk) (pk, p1) 就是它的所有border, 其中任何一条边 (p[j], p[(j+1)%n]) 与也只与另外一个region’ 共享, 而region’ 做取边操作的时候, 这条共享边是颠倒的, 即 (p[(j+1)%n], p[j]) , 所以构造一个二维数组p[][], 上下三角形是对称的, 一对对称的元素就代表了相连的两个区域
club就存在所有靠着它的region内, 在这些region里面此club的步数都是0
细节:
以后这种繁题把变量名起的明白一点.. 多写点注释, 不然容易糊涂, 不太好写函数(其实可以.. 懒)
110行, 跑47ms, 还不错的样子..
Update: 这题数据比较弱, 用floyd简便很多, 因为为BFS准备比较麻烦, floyd直接开个数组全∞了事.. 复杂度N3
代码点下面 (没有任何可读性可言..)
Continue reading
a = (b*c-1)/(b+c) 令m = b+c => c = m-b
推得 m = – (b^2 + 1)/(a – b)
做一下多项式除法后 m = (b – a) + (a^2 + 1)/(b – a) + 2a
所以令k=b – a (由arctan()的函数图像知k>0)
=> m = k + (a^2 + 1)/k + 2a
根据函数图像知道 (0 , 根号(a^2 + 1)]内递减, [根号(a^2 + 1), +∞)内递增, 所以我们需要求两个区间上最靠近根号(a^2 + 1)的使m为整数的k
设 i>=根号(a^2 + 1) 则对于此情况下要求的mi = i + (a^2 + 1)/i + 2a 有 j = (a^2 + 1)/i 使
mi = (a^2 + 1)/j + j + 2a
而 j<=根号(a^2 + 1) 所以右边区间满足情况的i在左边都能找到对应的j, 所以只要搜索左边就行了
k=n..1
找出最先使 (a*a+1)%k==0的k即可
[cpp]
#include <stdio.h>
int main() {
int a;
scanf("%d",&a);
int k=a;
long long foo=(long long)a*a+1;
while(foo%k)
k–;
printf("%d\n",k+foo/k+2*a);
return 0;
}
[/cpp]
无意看到的题目.. 因为是中文的就猫了一眼, 觉得挺水就做做, 结果一做就是一下午.. NOI还有点名堂
开始觉得就是博弈+简单DP, 右图每一个格子 (a, b) , 玩家一次取石子以后能变成的状态是 (a-i, b) , (a, b-i) , 或者 (a-i, b-i) , 只要路线上存在lose, 赋值为win, 否则赋值lose. 整个表格是对称的. 自底向上DP就可以解决.
然后看了discuss, 存在O(1) 的算法..
Beatty sequence Wiki 讲解 , 看一下就了了..
The positive irrational number
generates the Beatty sequence
If
then
is also a positive irrational number. They naturally satisfy
and the sequences
and
form a pair of complementary Beatty sequences.
For r = the golden mean, we have s = r + 1. In this case, the sequence
, known as the lower Wythoff sequence, is
and the complementary sequence
, the upper Wythoff sequence, is
上下两个数列整好组成 lose 状态的坐标 (1,2) (3,5) (4,7) … 至于为什么等我有空会思考update一下 =D 好神奇阿
其中r是黄金分割律, 即 (1+sqrt(5))/2
则如果m在第一个数列里,则
m=[nr]=nr-x
m/r=n-x/r
其中x属于[0,1) , 先求出n再判断m/r是否在等式右边的区间里即可. 再返回n判断输入的b是否在二队列中相应的位置
Code:
[cpp]
#include <stdio.h>
#include <math.h>
#include <algorithm>
//return num in Beatty sequence(r=golden mean), -1 if not belong to
int Br(int m) {
static const double P=(1+sqrt(5.0))/2;
double foo=m/P;
int n=(int)foo;
if(foo-n>0.999999)
n++;
n++;
if(foo>(n-1/P))
return n;
else
return -1;
}
int main() {
int a,b;
while(scanf("%d%d",&a,&b)!=EOF) {
if(a>b)
std::swap(a,b);
int foo=Br(a);
bool win=true;
if(foo!=-1)
if(a+foo==b)
win=false;
if(win)
printf("1\n");
else
printf("0\n");
}
return 0;
}
[/cpp]
以后不好意思放报告就在这记一下心得啦
思路和网上的都差不多, 我另外开了程序算出每一行可能的情况直接copy进 stack[] 中..耍流氓.. 看起来直观点
引用一下大牛BYVoid的思路, 不自己写了
较难看出的动态规划问题。注意到数据范围N≤100；M≤10，发现每行的宽度都不大，所以可以考虑把一行看成一个状态，表示该行的布置方案。每行的布置方案可以预先处理出，由数学知识可以算出，每行最多的布置方案数也不过60个而已。
状态设定
F[i,a,b]为前i行，第i行的方案为A[a]，第i-1行的方案为A[b]的最大炮兵数。
状态转移方程
- F[i,a,b]=Max{ F[i-1,b,c] + P[a] }
其中c为i-2行的布置方案，a,b,c应保证互不冲突，即放置方案中炮兵都在平地上，且不会互相攻击到。
目标结果
- Ans=Max{F[N,a,b]}
中间进行过一次错误的优化, 认为如果, 比如
画个图..
1001比1101少了一个1, 那么1101得出的结果至少不会比1001差, 可以剪掉1001. 比如上图的第三行, 没有炮的情况就可以省去,.我当时的想法是如果省掉第三行的炮, 放在第四行唯一的P上(其他情况也是相似), 第四行以下面临的情况就会比之前更加严峻, 从而不会得出更好的结果, 顶多一样.
但是我并没有考虑第三行能对第一行也产生影响 (造成这个错误的原因是状态压缩DP只记录近两行. 虽然没有明面上写, 但是情况已经记录在得分中了). 第三行的P不放炮, 则第一行和第四行都能放, 结果就更好了.
我写成这样
[cpp]public:
int *(a[60]);
State (int m=0) {
M=m;
for(int i=0;i<stackN;i++) {
a[i]=new int[stackN];
memset(a[i],0xff,sizeof(int)*stackN);
}
}[/cpp]
能够compile, 在另开的程序里也没有问题, 但是在题目中答案就不一样, 我跟踪了, 在 s[i].dp(s[i-1]) 的过程中 s[i-1].a[][] 会莫名发生改变, 实际上又没有对它进行任何操作. 值得一提的是release和debug得出的答案不一样, 根据经验应该是内存的什么问题.. 也有可能是类里动态分配内存就不对头, 因为在类中定义变量不能用new.. 开学去问问看
Code: (其实是我第一次用类.. 这个问题有点绕, 于是尝试封装=D )
这是所谓的二叉树么.. 算法很简单, 只是因为第一次用这种结构体封装, 还是试了很多次才摸索出来的.. 很好用诶! 记一下
细节.. 地址和变量不要搞混了.. fw?fw->v():false 我写成了fw->v()? 错了好久
[cpp]#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct Orz {
Orz *fw,*fx;
bool (*f)(bool w,bool x);
bool v() {
return (*f)(fw?fw->v():false,fx?fx->v():false);
};
bool p[5];
char sb[]={‘K’,’A’,’C’,’E’,’N’,’p’,’q’,’r’,’s’,’t’};
char input[201];
int count;
bool fK(bool w,bool x) { return w&x; }
bool fA(bool w,bool x) { return w|x; }
bool fC(bool w,bool x) { return !(w&&!x); }
bool fE(bool w,bool x) { return !(w^x); }
bool fN(bool w,bool x) { return !w; }
bool fp(bool w,bool x) { return p[0]; }
bool fq(bool w,bool x) { return p[1]; }
bool fr(bool w,bool x) { return p[2]; }
bool fs(bool w,bool x) { return p[3]; }
bool ft(bool w,bool x) { return p[4]; }
bool (*f[])(bool w,bool x)={fK,fA,fC,fE,fN,fp,fq,fr,fs,ft};
Orz *proc() {
char a=input[count++];
Orz *node=(Orz *)malloc(sizeof(Orz));
node->fw=node->fx=NULL;
int type;
for(type=0;sb[type]!=a;type++);
node->f=f[type];
if(type<=4)
node->fw=proc();
if(type<4)
node->fx=proc();
return node;
}
int pow2(int n) {
int r=1;
for(int i=0;i<n;i++)
r*=2;
return r;
}
int main() {
while(1) {
gets(input);
if(input[0]==’0′)
break;
count=0;
Orz *bigBang=proc();
short tester;
for(tester=0x0000;tester<=0x001f;tester++) {
for(int i=0;i<5;i++)
p[i]=tester/pow2(i)%2;
if(bigBang->v()!=true)
break;
}
if(tester==0x0020)
printf("tautology\n");
else
printf("not\n");
}
return 0;
}
[/cpp]
求严格背包, 这次要求是所有物品都必须使用, 问有多少种填满的方法(具体看题)
如果只问能否填满(这样看来又不能把v=重量*杠杆长度看成物品了, 不是传统背包..好难归纳) 那只要用bool型数组记录, 因为不能不用 所以用两个数组更替(a0[i]==true doesn’t mean a1[i]==true, so.)
问有多少种方法把bool换成计数器即可
2010/08/05 Update:
在”能不能放满”(或者填满特定容量) 这种题型中, 以下三种情况是可以让我们求”符合要求的组合有多少种”
1. 一个物品具有多种可选的体积. 比如在本题中是”在物品体积可变, 并且能够为负的情况下, 能不能使占用空间恰为0(平衡)”
2. 物品可以选择不用
3. 1&&2
原因很简单, 上面三种情况的补集是”物品体积固定并且必须全用”, 这种情况最后占用的容积是常数, 逆否命题即上面的蓝字部分成立.
细节:
int *a=(int *)malloc(sizeof(int)*20001); //sizeof(a)==4
int a[20001]; //sizeof(a)==80004;
混淆了一下 导致数组不能初始化, 结果是诡异的3 (答案是2)
debug的时候数组里是非常混乱的 (比如a0[9999]==-265219901)
但是release的时候数组即使不初始化也都为0, 但不一定(诡异的3就是因为某个数==1, 应该初始化为0的, 和内存前面的写入有关吧)
代码:
[cpp]#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main() {
int *a0,*a1;
int C,G,c[20],g[20];
a0=(int *)malloc(sizeof(int)*20001);
memset(a0,0x00,sizeof(int)*20001);
a0[10000]=1;
scanf("%d%d",&C,&G);
for(int i=0;i<C;i++)
scanf("%d",c+i);
for(int i=0;i<G;i++)
scanf("%d",g+i);
int v;
for(int i=0;i<G;i++) {
a1=(int *)malloc(sizeof(int)*20001);
memset(a1,0x00,sizeof(int)*20001);
/*/debug
for(int k=9900;k<=10100;k++)
if(a0[k])
printf("a0[%d]=%d, ",k,a0[k]);
printf("\n");//*/
for(int j=0;j<C;j++) {
v=g[i]*c[j];
for(int i=19000;i>=1000;i–) //order doesn’t make sense.
a1[i+v]+=a0[i];
/*/debug
for(int k=9900;k<=10100;k++)
if(a1[k])
printf("a1[%d]=%d, ",k,a1[k]);
printf("\n");//*/
}
free(a0);
a0=a1;
}
printf("%d\n",a0[10000]);
return 0;
}
[/cpp]
